Unit 6 homework 9 geometric sequences answer key – Embark on a mathematical journey with our in-depth analysis of Unit 6 Homework 9: Geometric Sequences Answer Key. This comprehensive guide unravels the intricacies of geometric sequences, empowering you with a profound understanding of their properties and applications.
Delve into the fundamental concepts, master the formulaic intricacies, and explore the practical implications of geometric sequences. Our meticulously crafted explanations and illustrative examples will illuminate your path to mathematical mastery.
Geometric Sequences: Definition and Formula
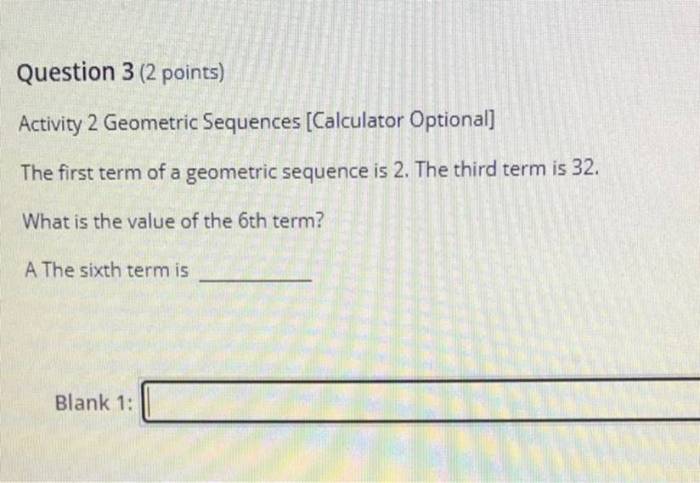
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a constant value called the common ratio. The formula for the nth term of a geometric sequence is:
$$a_n = a_1 \cdot r^n-1$$
where
- $a_n$ is the nth term of the sequence
- $a_1$ is the first term of the sequence
- $r$ is the common ratio
- $n$ is the number of the term
For example, the sequence 2, 6, 18, 54, … is a geometric sequence with a common ratio of 3 and a first term of 2.
Common Ratio and First Term: Unit 6 Homework 9 Geometric Sequences Answer Key
The common ratio of a geometric sequence is the constant value by which each term is multiplied to obtain the next term. It determines the rate at which the sequence grows or decays.
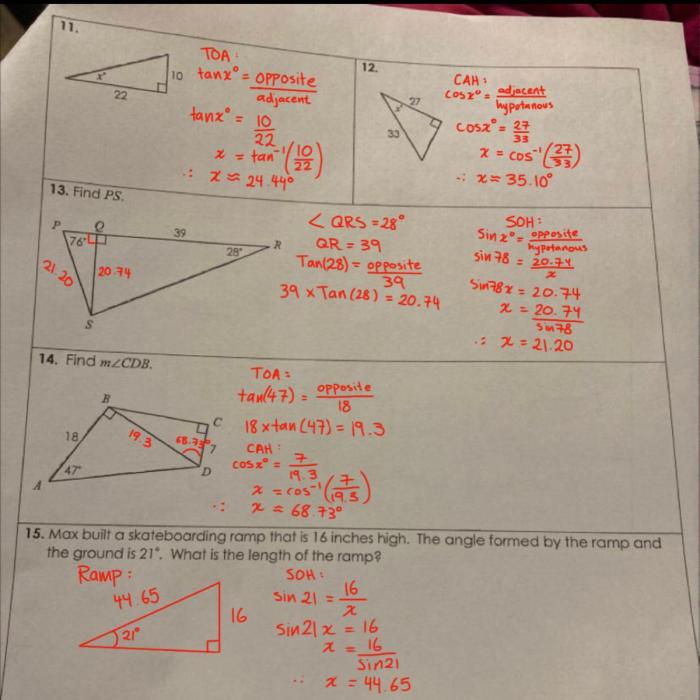
The first term of a geometric sequence is the initial value of the sequence. It establishes the starting point from which the sequence is generated.
For example, in the sequence 2, 6, 18, 54, …, the common ratio is 3 and the first term is 2. This means that each term is obtained by multiplying the previous term by 3, starting from the first term of 2.
Sum of a Geometric Sequence

The sum of a finite geometric sequence is given by the formula:
$$S_n = \fraca_1(1-r^n)1-r$$
where
- $S_n$ is the sum of the first $n$ terms of the sequence
- $a_1$ is the first term of the sequence
- $r$ is the common ratio
- $n$ is the number of terms
The sum of an infinite geometric series converges if $|r|< 1$, and diverges if $|r| \geq 1$.
Applications of Geometric Sequences
Geometric sequences have numerous applications in various fields, including:
- Modeling population growth and decay
- Calculating compound interest
- Solving problems involving exponential growth and decay
- Analyzing fractals and other geometric patterns
Key Questions Answered
What is the formula for the nth term of a geometric sequence?
a_n = a_1 – r^(n-1)
How do you find the common ratio of a geometric sequence?
r = a_n / a_(n-1)
What are the conditions for convergence and divergence of a geometric series?
– Convergent: |r|< 1 - Divergent: |r| ≥ 1
